COMPARATIVE BAYESIAN AND CLASSICAL ESTIMATION OF THE SCALE PARAMETER IN THE WEIBULL POWER FUNCTION DISTRIBUTION
DOI:
https://doi.org/10.33003/fjs-2025-0912-4454Keywords:
Weibull exponential distribution, Maximum likelihood estimation, Bayesian estimation, Gamma prior, Jeffrey priorAbstract
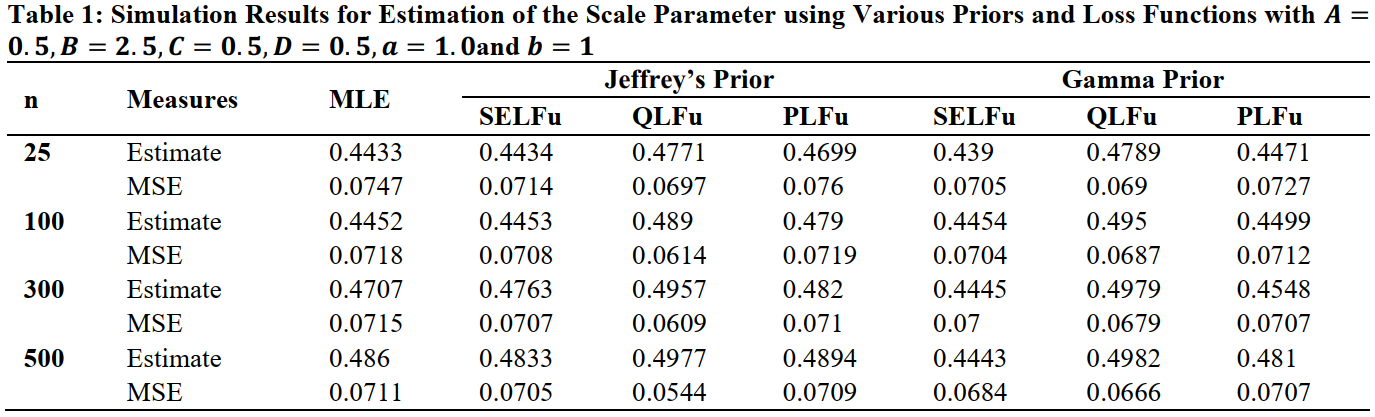
We investigate the scale parameter of the Weibull power function distribution (WPFD) via both Bayesian and traditional statistical methodologies. Diverse estimations for the scale parameter were derived from the Bayesian framework, employing three distinct loss functions. The findings revealed that quadratic loss functions, utilising Jeffrey's and Gamma priors, consistently yielded better results than precautionary and squared error loss functions, irrespective of sample size. As the sample size increased, the estimation errors diminished, and the calculated values converged towards the true scale parameter. In conclusion, the Bayesian estimates for the scale parameter, particularly those utilising Jeffrey's and Gamma priors with a quadratic loss function, demonstrated superior performance compared to other estimation techniques
References
Abd Elgawad, M. A., Usman, A., Doguwa, S. I., Sadiq, I. A., Zakari, Y., Ishaq, A. I., ... & Hashem, A. F. (2025). A hybrid Log-Logistic-Weibull Regression Model for survival analysis in leukaemia patients and radiation data. Journal of Radiation Research and Applied Sciences, 18(3), 101836.
Adepoju A. A., Abdulkadir S. S., Jibasen D. (2024c). On Different Classical Estimation Approaches for Type I Half Logistic-Topp-Leone-Exponential Distribution. Reliability: Theory & Applications. 1(77):577-587.
Adepoju A. A., Abdulkadir S. S., Jibasen D., Olumoh J. S. (2024a). Type I Half Logistic Topp-Leone Inverse Lomax Distribution with Applications in Skinfolds Analysis. Reliability: Theory & Applications. 1(77), 618-630.
Adepoju A. A., Bello A. O., Isa A. M., Adesupo A., & Olumoh J. S. (2024d). Statistical inference on the sine-exponential distribution parameter. Journal of Computational Innovation and Analytics, 3(2), 129-145. https://doi.org/10.32890/jcia2024.3.2.6
Adepoju A. A., Isa A. A., Magaji A. A., Nasir M. S., Aliyu A. M. (2021b, 158-167). Preference of Bayesian techniques over classical techniques in estimating the scale parameter of the inverse Rayleigh Frechet distribution. Royal Statistical Society Nigeria Local Group 2021 Conference Proceedings.
Adepoju A. A., Isa A. M., Bello A. O. (2024b). Cosine Marshal-Olkin-G Family of Distribution: Properties And Applications. RT&A, No 3 (79) Volume 19, September
Adepoju A. A., Usman M., Alkassim R. S., Sani S. S., Adamu K. (2021a, 182-190). Parameter (shape) Estimation of Weibull-Exponential Distribution Using Classical and Bayesian Approach Under Different Loss Functions, Royal Statistical Society Nigeria Local Group Conference Proceedings.
Adepoju, A. A., Abdulkadir, S. S., & Jibasen, D. (2023). The Type I Half Logistics-Topp-Leone-G Distribution Family: Model, Its Properties and Applications. UMYU Scientifica, 2(4), 09 – 22.
Alduais, F. (2021). Comparison of classical and Bayesian estimators to estimate the parameters in the Weibull distribution under a weighted general entropy loss function. International Journal of Advanced and Applied Sciences, 8(3), 57-62.
Aliyu, Y. and Yahaya, A. (2016). Bayesian estimation of the shape parameter of the generalised Rayleigh distribution under a non-informative prior. International Journal of Advanced Statistics and Probability, 4 (1), 1-10.
Bello O., A.,Doguwa S., I., Yahaya A., Jibril H., M. (2020). A Type I Half Logistic Exponentiated-G Family of Distributions: Properties and Application, Communication in Physical Sciences, 7(3):147-163.
Bello O., A.,Doguwa S., I., Yahaya A., Jibril H., M. (2021). A Type II Half Logistic Exponentiated-G Family of Distributions with Applications in Survival Analysis, FUDMA Journal of Science, 5(3):177-190.
Danrimi, M. L. and Abubakar, A. (2023). A Bayesian Framework for Estimating Weibull Distribution Parameters: Applications in Finance, Insurance, and Natural Disaster Analysis, UMYU Journal of Accounting and Finance Research, 5(1): 64–83. https://doi.org/10.61143/umyu-jafr.5(1)2023.006
Dey, S., & Maiti, S. S. (2010). Bayesian estimation of the parameter of the Maxwell distribution under different loss functions. Journal of Statistical Theory and Practice, 4(2), 279-287.
Eraikhuemen, I. B., Bamigbala, O. A., Magaji, U. A., Yakura, B. S. and Manju, K. A. (2020a). Bayesian Analysis of Weibull-Lindley Distribution Using Different Loss Functions. Asian Journal of Advanced Research and Reports, 8(4), 28-41.
Eraikhuemen, I. B., Mohammed, F. B. and Sule, A. A. (2020b). Bayesian and Maximum Likelihood Estimation of the Shape Parameter of Exponential Inverse Exponential Distribution: A Comparative Approach. Asian Journal of Probability and Statistics; 7(2), 28-43.
Habu, L., Usman, A., Sadiq, I. A., & Abdullahi, U. A. (2024). Estimation of Extension of Topp-Leone Distribution using Two Different Methods: Maximum Product Spacing and Maximum Likelihood Estimate. UMYU Scientifica, 3(2), 133–138. https://doi.org/10.56919/usci.2432.014
Hassan E. A. A., Elgarhy M., Eldessouky E. A., Hassan O. H. M. Amin E. A. Almetwally, E. M. (2023). Different Estimation Techniques for a New Probability Distribution Approach Based on Environmental and Medical Data. Axioms, 12, 220.
Ieren, T. G. and Oguntunde, P. E. (2018). A Comparison between Maximum Likelihood and Bayesian Estimation Methods for a Shape Parameter of the Weibull-Exponential Distribution. Asian Journal of Probability and Statistics, 1(1): 1-12.
Ieren, T. G., Chama, A. F., Bamigbala, O. A., Joel, J., Kromtit, F. M., & Eraikhuemen, I. B. (2020). On A Shape Parameter of Gompertz Inverse Exponential Distribution Using Classical and Non-Classical Methods of Estimation. Journal of Scientific Research & Reports, 25(6): 1-10.
Isa A. M., Kaigama A., Adepoju A. A., Bashiru S. O. (2023) Lehmann Type II-Lomax Distribution: Properties and Application to Real Data Set. Communication in Physical Sciences, 9(1):63 – 72
Ishaq, A. I., Abiodun, A. A., & Falgore, J. Y. (2021). Bayesian estimation of the parameter of the Maxwell-Mukherjee Islam distribution using assumptions of the Extended Jeffreys, Inverse-Rayleigh and Inverse-Nakagami priors under the three loss functions. Heliyon, 7(10).
Kajuru, J. Y., Dikko, H. G., Mohammed, A. S., & Fulatan, A. I. (2023). Odd GompertzGFamily of Distribution, Its Properties and Applications. FUDMA JOURNAL OF SCIENCES, 7(3), 351-358.
Liu, X., Arslan, M., Khan, M., Anwar, S.M., and Rasheed, Z. (2021). Classical and Bayesian Estimation of Two-parameter Power Function Distribution https://doi.org/10.20944/preprints202108.0222.v1d
Mohammed, A. A., Hamdani, H., Zakari, Y., Abdullahi, J., Sadiq, I. A., Ouertani, M. N., ... & Elgarhy, M. (2025). On the Rayleigh Exponentiated Odd Generalised-Inverse Exponential Distribution With Properties and Applications. Engineering Reports, 7(11), e70457.
Mohammed, U., Ibrahim, D. S., Sulaiman, M. A., David, R. O., & Abubakar, S. I. (2025). Development of Topp-Leone Odd Fréchet Family of Distribution with Properties and Applications. Communication In Physical Sciences, 12(4), 1214-1226.
Obafemi, A. A., Usman, A., Sadiq, I. A., & Okon, U. (2024). A New Extension of Topp-Leone Distribution (NETD) Using Generalised Logarithmic Function. UMYU Scientifica, 3(4), 127–133. https://doi.org/10.56919/usci.2434.011
Oguntunde, P. E., Balogun, O.S., Okagbue, H.I., Bishop. S.A. (2015). The Weibull Exponential Distribution: Its Properties and Applications. Journal of Applied Sciences 15(11):1305-1311.
Preda, V., Eugenia, P. and Alina, C. (2010). Bayes Estimators of Modified-Weibull Distribution parameters using Lindley's approximation. WSEAS TRANSACTIONS on MATHEMATICS, 9 (7), 539-549.
Sadiq, I. A., Doguwa, S. I. S., Yahaya, A., & Garba, J. (2023c). New Generalized Odd Fréchet-Odd Exponential-G Family of Distribution with Statistical Properties and Applications. FUDMA Journal of Sciences, 7(6), 41-51. https://doi.org/10.33003/fjs-2023-0706-2096
Sadiq, I. A., Doguwa, S. I. S., Yahaya, A., & Usman, A. (2023b). Development of New Generalized Odd Fréchet-Exponentiated-G Family of Distribution. UMYU Scientifica, 2(4), 169-178. https://doi.org/10.56919/usci.2324.021
Sadiq, I. A., Doguwa, S. I., Yahaya, A., & Garba, J. (2022). New Odd Frechet-G Family of Distribution with Statistical Properties and Applications. AFIT Journal of Science and Engineering Research, 2(2), 84-103.
Sadiq, I. A., Doguwa, S. I., Yahaya, A., & Garba, J. (2023a). New Generalized Odd Frechet-G (NGOF-G) Family of Distribution with Statistical Properties and Applications. UMYU Scientifica, 2(3), 100-107. https://doi.org/10.56919/usci.2323.016
Sadiq, I. A., Garba, S., Kajuru, J. Y., Usman, A., Ishaq, A. I., Zakari, Y., ... & Yahaya, A. (2024). The Odd Rayleigh-G Family of Distribution: Properties, Applications, and Performance Comparisons. FUDMA Journal of Sciences, 8(6), 514–527. https://doi.org/10.33003/fjs-2024-0806-3011
Sadiq, I. A., Kajuru, J. Y., Doguwa, S. I., Yahaya, G. Y., Hephzibah, A. A., Yahaya, S. S., ... & Bello, A. (2025b). Survival analysis in advanced lung cancer using Weibull survival regression model: estimation, interpretation, and clinical application. Journal of Statistical Sciences and Computational Intelligence Volume, 1(2), 106-123.
Sadiq, I. A., Zakari, Y., Doguwa, S. I., Isiya, M., Suleiman, S. Y., Ajayi, A. H., ... & Samuel, W. (2025a). Survival Analysis of Acute Myocardial Infarction Patients Using the Kumaraswamy-Logistic Model and Kaplan-Meier Estimation. Iraqi Statisticians Journal, 15-32.
Semary, H., Sadiq, I. A., Doguwa, S. I. S., Ishaq, A. I., Suleiman, A. A., Daud, H., & Abd Elgawad, M. A. (2025). Advancing survival regression using the NGOF exponentiated Weibull distribution for vesicovaginal fistula and radiation data applications. Journal of Radiation Research and Applied Sciences, 18(2), 101497. https://doi.org/10.1016/j.jrras.2025.101497
Tahir, M. H., Alizadeh, M., Mansoor, M., Cordeiro, G. M., et al. (2016). The Weibull-power function distribution with applications. Hacettepe Journal of Mathematics and Statistics, 45(1), 245-265.
Varian, H. R. (1975). A Bayesian approach to real estate assessment. Studies in Bayesian econometrics and statistics in honour of Leonard J. Savage.
Yilmaz A., Kara M., Ozdemir O. (2021). Comparison of different estimation techniques for extreme value distribution. Journal of Applied Statistics, 48, 13-15.
ZeinEldin R. A., Chesneau C, Jamal F., Elgarhy M. (2019). Different estimation techniques for Type I Half-Logistic Topp–Leone Distribution. Mathematics, 7, 985.
Zellner, A. (1986). Bayesian estimation and prediction using asymmetric loss functions. Journal of the American Statistical Association, 81(394), 446-451.
Downloads
Published
Issue
Section
Categories
License
Copyright (c) 2025 Ibrahim Abubakar Sadiq, Hauwa Abdulrahman Dangana, Abubakar Usman, Jamilu Garba

This work is licensed under a Creative Commons Attribution 4.0 International License.




