COMPARATIVE ANALYSIS OF THE TRANSMISSION COEFFICIENTS OF THE 1D RECTANGULAR POTENTIAL BARRIER FOR Ge, Si, GaAs & Al0.37Ga0.63As

Abstract

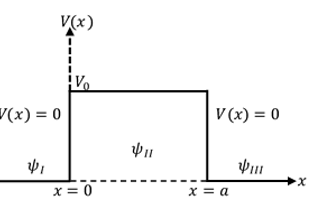
Python programming is used in the comparative analysis of the transmission coefficients, T, as function of barrier width, “a”, barrier height “V₀”, and particle energy “E”. These variables are chosen in pairs of various combinations, while keeping one of the variables a constant. Four semiconductor materials types [Germanium (Ge), Silicon (Si), Gallium Arsenide (GaAs) and Aluminum Gallium Arsenide (Al_0.37Ga_0.63As)] are chosen and the idealized 1D rectangular single-barrier potential is used as the model. Results show that increasing the particle energy enhances tunneling probability, leading to peaks of 0.79, 0.55, 0.46 and 0.36 at energies 0.50eV for Ge, 0.88eV for Si, 1.19eV for GaAs and 1.69eV for Al_0.37Ga_0.63As respectively which may indicate resonance. Moreover, irrespective of the choice of (E, V_o) for each material, the transmission coefficient typically decreases exponentially with the increase in the barrier width. This study further reveals that intrinsic semiconductor materials (Ge, Si) support higher tunneling, whereas semiconductor heterostructures (GaAs, Al_0.37Ga_0.63As) suppress transmission. There is a hierarchy of tunneling efficiency across the materials i.e. , which may serve as a pointer in the design of devices such as resonant tunneling diodes, quantum cascade lasers, and tunneling transistors.