INFLUENCE OF MAGNETIC FIELD AND NANOPARTICLE TRANSPORT ON BOUNDARY LAYER FLOW: A NUMERICAL INVESTIGATION
DOI:
https://doi.org/10.33003/fjs-2026-1001-4539Keywords:
Magnetohydrodynamics, Nanofluid, Heat and Mass Transfer, Exponentially Fitted Block Method, Thermal Radiation, Nanoparticle TransportAbstract
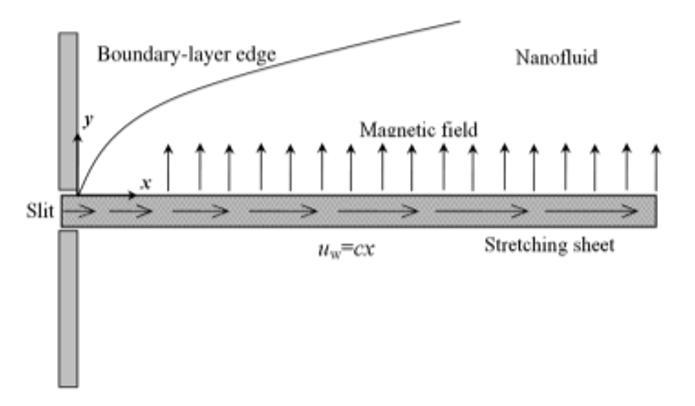
A study of magnetic field and nanoparticle transport on boundary layer flow of magnetohydrodynamic (MHD) nanofluid over a stretching vertical surface has been analyses numerically. By introducing appropriate similarity variables, the governing partial differential equations describing momentum, energy and concentration were reduced to nonlinear coupled Ordinary Differential Equations (ODE). Utilizing the shooting technique along exponentially fitted Simpson type block method is used to solve the Boundary value problems using computational software MAPLE 16. Numerical results for velocity, temperature and concentration profiles are presented and the effect of key parameters including magnetic field strength, Brownian motion, thermophoresis, internal heat generation and thermal radiation was analyzed. The computed Nusselt number and Sherwood number demonstrate excellent agreement with existing literature, confirming the stability and accuracy of the method used. The results reveal that magnetic effects reduce fluid velocity while thickening thermal and concentration boundary layers, whereas buoyancy forces, radiation and internal heat generation enhance momentum and heat transport. Nanoparticle diffusion is significantly influenced by thermophoresis and Brownian motion effects
References
Abbas, T. (2025). Slip effects and Lorentz force impacts on chemically reactive hybrid nanofluid over an exponentially stretching sheet. International communications in heat and mass transfer, i60, 108214. Doi.org/10.1016/j.icheatmasstransfer.2024.108214.
Arshad, M., Ahmed, A., & Hassan, A. (2024). Mixed convective hybrid nanofluid flow a stretching surface with joule heating and non-uniform heat source effects. Journal of magnetism and magnetic material, 592, 171805. Doi.org/10.1016/j.jmmm.204.171805.
Cengel, Y. A., & Ghajar, A. J. (2015). Heat and mass transfer: Fundamentals and applications (5th ed.). McGraw-Hill Education.
Choi, S.U.S., & Eastman, J. A. (1995). Enhancing thermal conductivity of fluids with Nanoparticles. In D.A. Siginer & H.P. Wang (Eds), Developments and Applications of Non-Newtonian flow, 231, 99-105.
Davidson, P. A. (2017). Introduction to magnetohydrodynamics (2nd ed.). Cambridge University Press.
Faniyi, O. E., Modebei M.I., & Olaiya, O.O. (2023). A three- step Simpson’s type exponentially fitted backward difference method for the numerical solution of first order ordinary differential equations. Journal of the Nigerian mathematical society. 42(3), 273-285.
Khan, K., Javed, M., Ullah, M., & Riaz, M. (2023). Heat and mass transport analysis for Williamson MHD nanofluid flow over a stretched sheet. Elsevier, DOI: 10.1016/j.rinp.2023.106873.
Kho, Y., Hussanan, A., Sarif, N., & Ismail, Z. (2018). Thermal radiation effects on MHD with flow heat and mass transfer in casson nanofluid over a stretching sheet. MATEC web of conference, 150(2018), DOI:10.1051/matecconf/201815006036.
Kumar, R. Sravani, J., & Rao, V.S. (2025). Entropy generation and thermal stability of MHD Casson nanofluid flow over a porous surface for solar energy applications. Case studies in thermal engineering, 65, 105421. Doi.org/10.1016/j.csite. 2024.105421.
Kwari, A. I., Sirisena, U. N., & Thomas, R. (2021). A block method for the numerical solution of second-order boundary value problems in fluid flow. Alexandria Engineering Journal, 60(6), 5627–5637.
Noghrehabadi, A., Pourrajeb, R., & Mohammad, G. (2012). Effect of Partial Slip Boundary Condition on the Flow and Heat Transfer of Nanofluids Past Stretching Sheet Prescribed Constant Wall Temperature. International Journal of Thermal Science, 54(2012), 253-261.
Olabode, B.T., Momoh, A.L., & Senewo, E.O. (2024). Derivative block methods for fourth order boundary value problems of ordinary differential equations. Proceedings of the Nigerian society of physical sciences conferences, 1(2024), DOI:10.61298/pnspsc.2024.1.80.
Omokhuale, E., & Uwanta, I.J. (2016). Viscoelastic Fluid follow with Heat and Mass Transfer in the Presence of Induced Magnetic filled. International Journal of Science for Global Sustainability, 2(3), 88-99.
Oyelakin, I., Adeyeye, O., Sibanda, P., & Omar, Z. (2020). On a New Block Method for an MHD Nanofluid flow with an Exponentially Decaying Internal Heat Generation. International Journal Numerical Method Fluids. 93(2021), 1816-1824.
Pavithra R. Venkatesh, P., & Reddy, G.J. (2025). Influence of nanoparticle shape factors on MHD nanofluid flow over a stretching sheet. A statistical and numerical approach. Numerical heat transfer Part A: applications, 87(2), 145-163.
Phang, P.S., & Abdulmajid, Z. (2015). Solving boundary layer problem using fifth order block method. AIP conference proceedings, DOI:10.1063/1.4913012.
Rashidi, M. M., Yang, Z., Bhatti, M. M., & Abbas, M. A. (2018). Heat and mass transfer analysis on MHD blood flow of Casson fluid model due to peristaltic wave. Thermal Science, 22(6A), 2439–2448.
Sadighi, S., Afshar, H., Jabbari, M., & Ashtiani, H. (2023). Heat and mass transfer for MHD nanofluid flow on a porous stretching sheet with prescribing boundary conditions. Cas studied in thermal Engineering Elsevier,49(1), DOI: 10.1016/j.csite.2023.103345.
Uddin, M., Sohail, A., Beg, O., & Ismail, A. (2017), Numerical solution of MHD slip flow of a nanofluid past a radiating plate with Newtonian heating. A lie group approach. Alexandria Engineering journal Elsevier, 57(2018), 2455-2464.
Usman, S. & Sulaiman, S. (2023). Heat and Mass transfer analysis for the MHD flow of Casson nanofluid in the presence of thermal radiation. FUDMA journal of science, 7(2), 188-198
Downloads
Published
Issue
Section
Categories
License
Copyright (c) 2026 Odunayo M Adekoya, Olusheye A Akinfenwa, Olugbenga J. Fenuga

This work is licensed under a Creative Commons Attribution 4.0 International License.




