NUMERICAL INVESTIGATION OF NONLINEAR DISPERSIVE WAVE STRUCTURES IN THEROSENAU – HYMAN AND GILSON–PICKERING EQUATIONS
DOI:
https://doi.org/10.33003/fjs-2025-0912-4405Keywords:
Rosenau–Hyman equation, Gilson–Pickering equation, nonlinear dispersion, soliton, compacton, spectral collocation method, numerical analysisAbstract
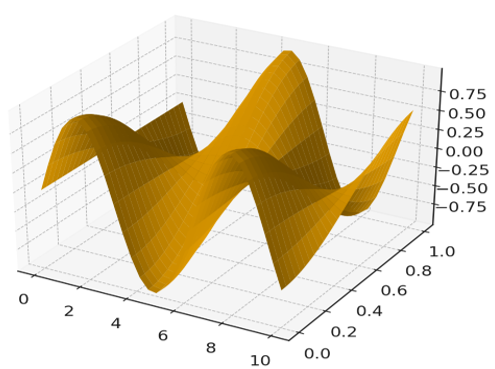
This paper investigates the nonlinear Gilson–Pickering equation, a model unifying several key dispersive equations. We employ to derive a new numerical approach and diverse family of exact traveling wave solutions. These solutions include bright solitons, dark solitons, singular solitons, and periodic solutions, which generalize and extend previously known results(Akgül et al., 2020, Ak et al., 2016& Barretta et al., 2004).The physical characteristics of the obtained solutions are analyzed graphically, providing insight into the wave dynamics governed by the equation. Our results confirm the efficacy of the chosen method and enrich the set of analytical solutions available for this important class of nonlinear evolutionary equations.
References
Adebisi,A. F., Okunola K. A., (2025); A Laguerre-Perturbed Galerkin Method For Numerical Solution Of Higher-Order Nonlinear Integro-Differential Equations, Fudma Journal Of Sciences (Fjs) Issn Online: 2616-1370 Issn Print: 2645 - 2944 Vol. 9 No. 11, November, 2025, Pp 238 – 242 Doi: Https://Doi.Org/10.33003/Fjs-2025-0911-3991
Ajibola, S. O., Oke, A. S., & Mutuku, W. N. (2020). LHAM approach to fractional order Rosenau-Hyman and Burgers' equations. Asian Research Journal of Mathematics, 16(6), 1–14.
Ak, T., Battal Gazi Karakoc, S., & Triki, H. (2016). Numerical simulation for treatment of dispersive shallow water waves with Rosenau-KdV equation. The European Physical Journal Plus, 131(10), 1–15.
Ak, T., Dhawan, S., Battal Gazi Karakoc, S., Bhowmik, S. K., & Raslan, K. R. (2017). Numerical study of Rosenau-KdV equation using finite element method based on collocation approach. Mathematical Modelling and Analysis, 22(3), 373–388.
Akgül, A., Aliyu, A. I., Inc, M., Yusuf, A., & Baleanu, D. (2020). Approximate solutions to the conformable Rosenau-Hyman equation using the two-step Adomian decomposition method with Padé approximation. Mathematical Methods in the Applied Sciences, 43(13), 7632–7639.
Barretta, P. K., Caldas, C. S. Q., Gamboa, P., & Limaco, J. (2004). Existence of solutions to the Rosenau and Benjamin-Bona-Mahony equation in domains with moving boundary. Electronic Journal of Differential Equations, 2004(35), 1–12.
Benjamin, T. B., Bona, J. L., & Mahony, J. J. (1972). Model equations for long waves in nonlinear dispersive systems. Philosophical Transactions of the Royal Society of London. Series A, Mathematical and Physical Sciences, 272(1220), 47–78.
Bertozzi, A. L., & Pugh, M. (1996). The lubrication approximation for thin viscous films: Regularity and long time behavior of weak solutions. Communications on Pure and Applied Mathematics, 49(2), 85–123.
Bhowmik, S. K. (2014). Piecewise polynomial approximation of a nonlocal phase transitions model. Journal of Mathematical Analysis and Application, 420(2), 1069–1094.
Bhowmik, S. K., Belbakib, R., Boulmezaoudc, T. Z., & Mziou, S. (2014). Solving two dimensional second order elliptic equations in exterior domains using the inverted finite elements method. Computers & Mathematics with Applications, 67(10), 2027–2045.
Bhowmik, S. K., & Jakobin, A. K. (2022). High-accurate numerical schemes for Black–Scholes models with sensitivity analysis. Journal of Mathematics, 2022, Article 4488082.
Bochev, P. B., & Gunzburger, M. D. (2008). Least-squares finite element methods. Springer.
Boussinesq, J. V. (1877). Essai sur la theorie des eaux courantes [Essay on the theory of water flow]. In Memoires Presentes Par Divers Savants A L'Academie Des Sciences (Vol. 23, pp. 241–680). Paris, France.
Cardenas, A., Mihaila, B., Cooper, F., & Saxena, A. (2011). Properties of compacton–anticompacton collisions. Physical Review E, 83(6), 066705.
Chertock, A., & Levy, D. (2001). Particle methods for dispersive equations. Journal of Computational Physics, 171(2), 708–730.
Choo, S. M., Chung, S. K., & Kim, K. I. (2008). A discontinuous Galerkin method for the Rosenau equation. Applied Numerical Mathematics, 58(6), 783–799.
Chung, S. K. (1998). Finite difference approximate solutions for the Rosenau equation. Applicable Analysis, 69(2), 149–156.
Chung, S. K., & Ha, S. N. (1994). Finite element Galerkin solutions for the Rosenau equation. Applicable Analysis, 54(2), 39–56.
Cinar, M., Secer, A., & Bayram, M. (2021). An application of Genocchi wavelets for solving the fractional Rosenau-Hyman equation. Alexandria Engineering Journal, 60(6), 5331–5340.
Dag, I., & Ozer, M. N. (2001). Approximation of the RLW equation by the least square cubic B-spline finite element method. Applied Mathematical Modelling, 25(3), 221–231.
Dag, I., Saka, B., & Irk, D. (2006). Galerkin method for the numerical solution of the RLW equation using quintic B-splines. Journal of Computational and Applied Mathematics, 190(1-2), 532–547.
De Frutos, J., López-Marcos, M. A., & Sanz-Serna, J. M. (1995). A finite difference scheme for the K(2,2) compacton equation. Journal of Computational Physics, 120(2), 248–252.
Dehestani, H., Ordokhani, Y., & Razzaghi, M. (2019). On the applicability of Genocchi wavelet method for different kinds of fractional-order differential equations with delay. Numerical Linear Algebra with Applications, 26(5), e2259.
Dehestani, H., Ordokhani, Y., & Razzaghi, M. (2021). Combination of Lucas wavelets with Legendre–Gauss quadrature for fractional Fredholm–Volterra integro-differential equations. Journal of Computational and Applied Mathematics, 382, 113070.
Dhawan, S., Bhowmik, S. K., & Kumar, S. (2015). Galerkin-least square B-spline approach toward advection–diffusion equation. Applied Mathematics and Computation, 261, 128–140.
Fornberg, B., & Whitham, G. B. (1978). A numerical and theoretical study of certain nonlinear wave phenomena. Philosophical Transactions of the Royal Society of London. Series A, Mathematical and Physical Sciences, 289(1361), 373–404.
Gardner, C. S., Green, J. M., Kruskal, M. D., & Miura, R. M. (1967). Method for solving the Korteweg-de Vries equation. Physical Review Letters, 19(19), 1095–1097.
Gardner, L. R. T., Gardner, G. A., & Dogan, A. (1996). A least squares finite element scheme for the RLW equation. Communications in Numerical Methods in Engineering, 12(12), 795–804.
Gomez, H., & De Lorenzis, L. (2016). The variational collocation method. Computer Methods in Applied Mechanics and Engineering, 309, 152–181.
Helal, M. A. (2002). Soliton solution of some nonlinear partial differential equations and its applications in fluid mechanics. Chaos, Solitons & Fractals, 13(9), 1917–1929.
Ismail, M. S., & Taha, T. R. (1998). A numerical study of compactons. Mathematics and Computers in Simulation, 47(6), 519–530.
Iyiola, O. S., Ojo, G. O., & Mmaduabuchi, O. (2016). The fractional Rosenau–Hyman model and its approximate solution. Alexandria Engineering Journal, 55(2), 1655–1659.
Kardashov, V., Einav, S., Okrent, Y., & Kardashov, T. (2006). Nonlinear reaction–
Downloads
Published
Issue
Section
Categories
License
Copyright (c) 2025 Adebisi Ajimot . F, Kolawole Mutairu K., Babalola Olutola. O.

This work is licensed under a Creative Commons Attribution 4.0 International License.




