THREE-STEP BLOCK INTEGRATORS BASED ON TOP ORDER METHODS FOR SOLUTIONS OF STIFF CHEMICAL KINETICS PROBLEMS
DOI:
https://doi.org/10.33003/fjs-2026-1001-4331Keywords:
Top order methods, Three-Step Block Integrators, Chemical kinetics, Stability analysisAbstract
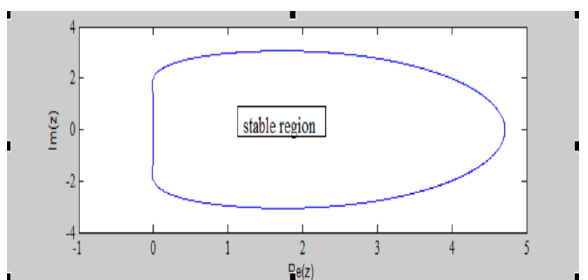
In this research, a three-step class of numerically stable block integrators based on top order methods was developed for solutions of stiff chemical kinetic problems. Firstly, the discrete schemes of the method were obtained from the same continuous formulation using the multistep collocation approach as block integrators. Secondly, Stability analysis of the newly derived method was carried out and it has shown to be consistent, zero-stable and A-stable. Numerical results were generated to investigate the influence of top order methods on stiff chemical kinetics problems. the results showed that the new method compare favourably with existing methods in the literature.
References
Abba I B 2019 Hybrid block extended second derivative backward differentiation formulae for the solution of stiff ordinary differential equations PhD Thesis Adamawa State university, Mubi, Nigeria.
Adoghe, L. O., Ukpebor, L. O., & Akhanolu, G. A. (2024). A NEW SECOND DERIVATIVE METHODS WITH HYBRID PREDICTORS FOR SOLVING STIFF AND NON-STIFF ORDINARY DIFFERENTIAL EQUATIONS. FUDMA JOURNAL OF SCIENCES, 8(4), 193-198.
Awari, Y. S., Taparki, R. & Kumleng, G. M., (2021). Second Derivative Block Type Top Order Method with Rodriguez Polynomial for Large Stiff and Oscillatory Systems. Recent Developments in the Solution of Nonlinear Differential Equations.
Bakari, A., Skwame, Y., & Kumleng, G. M. (2018). An Application of Second Derivative Backward Differentiation Formula Hybrid Block Method on Stiff Ordinary Differential Equations. Journal of Natural Sciences Research, 8(8), 2224-3186.
Brugnano, L., & Trigiante, D. (1998). Solving differential equations by multistep initial and boundary value methods. CRC Press.
Butcher, J. C. (2016). Numerical methods for ordinary differential equations. John Wiley & Sons.
Dahlquist, G. (1963). A special stability problem for linear multistep methods. BIT 3(1), 27-43.
Fatunla, S. O. (1988). Numerical methods for initial value problems in ordinary differential equations. Academic Press.
Fatunla, S. O. (1995). A class of block methods for second order IVPs. International journal of computer mathematics, 55(1-2), 119-133.
Joshua Sunday (2022). Optimized two-step second derivative methods for the solutions of stiff systems. Journal of Physics communications
Lambert, J. D. (1991). Numerical methods in ordinary differential equations (Vol. 146). New York: Wiley.
Ma’ali, A. I., Mohammed, U., Ben, A. G., & Jikantoro, Y. D. (2022). A Three-Step Numerical Approximant Based on Block Hybrid Backward Differentiation Formula for Stiff System of Ordinary Differential Equations. European Journal of Mathematics and Statistics, 3(3), 48-53.
Omar, Z., & Suleiman, M. (2005). Solving higher order ordinary differential equations using parallel 2-point explicit bock method. Matematika, 21(1), 15-23.
Onumanyi, P., Awoyemi, D. O., Jator, S. N., & Sirisena, U. W. (1994). New linear multistep methods with continuous coefficients for first order initial value problems. J. Nig. Math. Soc, 13(7), 37-51.
Yatim, S. A. M., Ibrahim, Z. B., Othman, K. I., & Suleiman, M. B. (2013). A numerical algorithm for solving stiff ordinary differential equations. Mathematical Problems in Engineering, 2013(1), 989381.
Yelwa, I. A., Galadima, J. I., Jikantoro, Y. D., & Yakubu, A. A. (2025). APPROXIMATE SOLUTIONS TO STIFF PROBLEMS OF THREE-STEP LINEAR MULTISTEP METHOD USING HERMIT POLYNOMIALS. FUDMA JOURNAL OF SCIENCES, 9(4), 234-238.
Downloads
Published
Issue
Section
Categories
License
Copyright (c) 2026 Anne Felix Katniyon, Kumleng, Geofrey Micah

This work is licensed under a Creative Commons Attribution 4.0 International License.




