THERMAL RADIATION AND CHEMICAL REACTION INFLUENCE ON MHD FLOW OF COUPLE STRESS FLUID PAST A VERTICAL PLATE
DOI:
https://doi.org/10.33003/fjs-2025-0912-4226Abstract
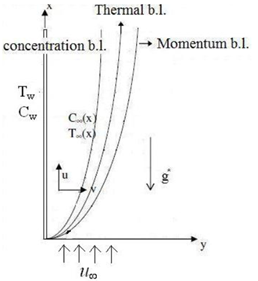
The behavior of fluids which incorporate microstructural effects like couple stresses, is of notable interest due to their relevance in various engineering, industrial, and biomedical applications. In this study, a comprehensive numerical investigation into the combined effects of thermal radiation and chemical reaction on magnetohydrodynamic (MHD) flow of a couple stress fluid past a vertical plate is presented. Through the application of similarity transformations, the governing equations are reduced to nonlinear ordinary differential equations. The transformed equations are solved using the BVP4C method in MATLAB, which is based on the Lobatto IIIa collocation technique, ensuring accurate and efficient numerical computations. The impact of the various parameters on velocity, temperature, and concentration within the boundary layer are illustrated graphically. Furthermore, numerical results for the local Nusselt number and Sherwood number are presented in tabular form to highlight the sensitivity of thermal and mass transport to these physical effects. The results reveal that an increase in the couple stress parameter significantly alters the fluid motion, reducing velocity near the plate and enhancing temperature and concentration profiles. Thermal radiation and magnetic field effects increase the temperature while reducing velocity, indicating energy retention and resistive electromagnetic forces. Chemical reaction reduce concentration due to reactant consumption, while Soret and Dufour effects display a complex interplay between thermal and concentration gradients. These findings not only provide physical insight into the flow behavior under multiple interactive influences but also offer valuable guidance for controlling heat and mass transfer in MHD systems involving complex non-Newtonian fluids.
References
Ahmed, S., Bég, O. A. and Ghosh, S. K. A. (2014). Couple stress fluid modeling on free convection oscillatory hydromagnetic flow in an inclined rotating channel, Ain Shams Engineering Journal, 5:1249-1265.
Ali, F., Sheikh, N. A., Khan, I. and Saqib, M. (2017). Magnetic field effect on blood f low of Casson fluid in axisymmetric cylindrical tube: a fractional model, J Magn Magn Mater., 423:327-336. https://doi.org/10.1016/j.jmmm.2016. 09.125.
Aparna, P. and Ramana, M. J. V. (2008). Oscillatory flow of an incompressible couple stress fluid past a permeable sphere, Proceedings of 53rd Congress ISTAM, Osmania University, India, 6:164-173.
Aparna, P., Ramana, M. J. V. and Sreelatha, K. (2007). Uniform flow of an incompressible couple stress fluid past a permeable sphere, International Electronic Engineering Mathematical Society, 8:1-10.
Awad, F., Haroun, N. A. H., Sibanda, P., Khumalo, M. (2016). On couple stress effects on unsteady nanofluid flow over stretching surfaces with vanishing nanoparticle flux at the wall, Journal Applied Fluid Mechanics, 9:1937 44. https://doi.org/10.18869/acadpub.jafm.68.235.24940.
Bég, A. O., Bhargava, R. and Rashidi, M. M. (2011). Numerical Simulation in Micropolar Fluid Dynamics, Saarbrücken: Lap Lambert Academic Publishing GmbH KG.
Bhatti, M. M., Zeeshan, A., Ellahi, R. and Shit, G. C. (2018). Mathematical modeling of heat and mass transfer effects on MHD peristaltic propulsion of two-phase f low through a Darcy-Brinkman-Forchheimer Porous medium, Advanced Powder Technol., 29:1189-1197. https://doi.org/10.1016/j.apt.2018.02.010.
Dawar, A., Shah, Z., Khan, W., Idrees, M. and Islam, S. (2019). Unsteady squeezing flow of magnetohydrodynamic carbon nanotube nanofluid in rotating channels with entropy generation and viscous dissipation, Adv Mech Eng., 11:1-18. https://doi.org/10.1177/1687814018823100.
Ellahi, R., Zeeshan, A., Shehzad, N. and Alamri, S. Z. (2018). Structural impact of Kerosene-Al2O3 nanoliquid on MHD Poiseuille flow with variable thermal conductivity: application of cooling process, J. Mol. Liquids, 264:607-615. https://doi.org/10.1016/j.molliq.2018.05.103.
Eringen, A. C. (1966). Theory of micropolar fluids, J Math Mech., 16:1–18. https://doi.org/10.1512/iumj.1967.16.16001.
Farroq, H., Ellahi, R., Zeeshan, A. and Vafai, K. (2018). Modelling study on heated couple stress fluid peristaltically conveying gold nanoparticles through coaxial tubes: a remedy for gland tumors and arthritis, Journal of Molecular Liquids, 268:149-155.
Hassan, A. R., Salawu, S. O. and Disu, A. B. (2020). The variable viscosity effects on hydromagnetic couple stress heat generating porous fluid flow with convective wall cooling, Scientific African, 9:e00495
Hayat, T., Awais, M., Safdar, A. and Hendi, A. A. (2012). Unsteady three dimensional f low of couple stress fluid over a stretching surface with chemical reaction, Nonlin. Analy. Mod. Cont., 17:47-59. https://doi.org/10.15388/NA.17.1.14077
Hayat, T., Iqbal, R., Tanveer, A. and Alsaed, A. (2016). Soret and Dufour effects in MHD peristalsis of pseudoplastic nanofluid with chemical reaction, J Mol Liq., 220:693-706. https://doi.org/10.1016/j.molliq.2016.04.123.24.
Hayat, T., Mustafa, M., Iqbal, Z. and Alsaedi, A. (2013). Stagnation-point flow of couple stress fluid with melting heat transfer, Appl Math Mech, 34:167-176. https://doi.org/10.1007/s10483-013-1661-97.
Khan, A., Shah, Z., Islam, S., Dawar, A., Bonyah, E., Ullah, H. and Khan, A. (2018). Darcy-Forchheimer flow of MHD CNTs nanofluid radiative thermal behaviour and convective non uniform heat source/sink in the rotating frame with microstructure and inertial characteristics, AIP Adv., 8:125024. https://doi.org/10.1063/1.5066223.31.
Khan, N. A., Aziz, S. and Khan, N. A. (2014). Numerical simulation for the unsteady MHD flow and heat transfer of couple stress fluid over a rotating disk, PLoS ONE, 9:e95423. https://doi.org/10.1371/journal.pone.0095423.
Kumam, P., Shah, Z., Dawar, A., Rasheed, H. U. and Islam, S. (2019). Entropy Generation in MHD radiative flow of CNTs casson nanofluid in rotating channels with heat source/sink, Math Problems Eng., 2019:9158093. https://doi.org/10.1155/2019/9158093.
Kumar, K. A., Reddy, J. V., Sugunamma, V. and Sandeep, N. (2019). Simultaneous solutions for MHD flow of williamson fluid over a curved sheet with nonuniform heat source/sink, Heat Transfer Res., 50:581–603. https://doi.org/10.1615/HeatTransRes.2018025939.
Lin, Y., Zheng, L., Zhang, X. and Chen, G. (2015). MHD pseudo-plastic nanofluids unsteady flow and heat transfer in a finite thin film over stretching sheet with internal heat generation, International Journal of Heat and Mass Transfer, 84:903-911. https://doi.org/10.1016/j.ijheatmasstransfer.2015.01.099.25.
Ramalakshmi, K. and Shukla, P. (2021). Creeping flow of couple stress fluid past a fluid sphere with a solid core, ZAMM, 101:e202000115.
Ramesh, K. and Devakar, M. (2015). The influence of heat transfers on peristaltic transport of MHD second grade fluid through porous medium in a vertical asymmetric channel, J Appl Fluid Mech. 8:351-365. https://doi.org/10.18869/acadpub.jafm.67.222.23471.26.
Ramkissoon, H. (1978). Drag in couple stress fluids, ZAMP- Journal of Applied Mathematics and Physics, 29:341-346.
Ramzan, M., Farooq, M., Alsaedi, A. and Hayat, T. (2013). MHD three-dimensional flow of couple stress fluid with Newtonian heating, Eur. Phys. J. Plus, 128:49-56. https://doi.org/10.1140/epjp/i2013-13049.
Reddy, M. G. and Reddy, K. V. (2015). Influence of Joule heating on MHD peristaltic f low of a nanofluid with compliant walls, Process Eng., 127:1002-1009. https://doi.org/10.1016/j.proeng.2015.11.449.
Rudolf, A. T., Baumjohann, W. and Balogh, A. (2014). The strongest magnetic fields in the universe: how strong can they become? Front Phys., 2:59. https://doi.org/10.3389/fphy.2014.0005923.
Shah, Z., Dawar, A., Alzahrani, E. O., Kumam, P., Khan, A. and Islam, S. (2019b). Hall effect on couple stress 3D nanofluid flow over an exponentially stretched surface with Cattaneo Christov Heat Flux Mode, IEEE Access., 7: 64844–55. https://doi.org/10.1109/ACCESS.2019.2916162
Shah, Z., Dawar, A., Kumam, P., Khan, W. and Islam, S. (2019a). Impact of nonlinear thermal radiation on MHD nanofluid thin film flow over a horizontally rotating disk, Appl. Sci., 9:153-163. https://doi.org/10.3390/app9081533.
Sreenadh, S., Kishore, S. N., Srinivas, A. N. S. and Reddy, R. H. (2011), MHD free convection f low of couple stress fluid in a vertical porous layer, Adv. Appl. Sci. Res., 2:215-222.
Srinivasacharya, D. and Kaladhar, K. (2012). Mixed convection flow of couple stress fluid in a non-darcy porous medium with Soret and Dufour effects, Journal of Applied Science and Engineering, 15:415-22.
Stokes, V. K. (1966). Couple stresses in fluids, Physics Fluids, 9:1709-1715.
Temple, R. C., Mihai, A. P., Arena, D. A. and Marrows, C. H. (2015). Ensemble magnetic behavior of interacting CoFe nanoparticles, Front Phys., 3:52. https://doi.org/10.3389/fphy.2015.00052.
Turkyilmazoglu, M. (2014). Exact solutions for two-dimensional laminar flow over a continuously stretching or shrinking sheet in an electrically conducting quiescent couple stress fluid, International Journal of Heat and Mass Transfer, 72:1-8. https://doi.org/10.1016/j.ijheatmasstransfer.2014.01.0098.
Uddin, Z. and Kumar, M. (2013). Hall and ion-slip effect on MHD boundary layer f low of a micro polar fluid past a wedge, Sci. Iran, 20:467-476. https://doi.org/10.1016/j.scient.2013.02.01330.
Downloads
Published
Issue
Section
Categories
License
Copyright (c) 2025 Feyisayo Ayorinde, B. I. Olajuwon, L. O. Sogbetun, M. O. Iyoko, M. T. Raji, O. Fagbemiro, B. U. Anyanwu

This work is licensed under a Creative Commons Attribution 4.0 International License.




