UNSTEADY MAGNETOHYDRODYNAMICS (MHD) FLOW OF FOURTH GRADE FLUID BETWEEN HORIZONTAL STATIONARY PLATES WITH VISCOUS DISSIPATION AND SUCTION EFFECTS

Authors

  • Nasiru T. Zakari
    Nigerian Defence Academy, Kaduna
  • Ayankop E. Andi
    Department of Mathematical Sciences, Kaduna State University, Kaduna, Nigeria
  • Joseph K. Moses
    Department of mathematics, Air force Institute of Technology, Kaduna, Nigeria
  • Wachin A.A
    Department of Mathematics, Nigerian Institute of Transport Technology, Zaria, Nigeria
  • Joshua B. Hassan
    Department of Mathematics, Nigerian Institute of Transport Technology, Zaria, Nigeria

Keywords:

MHD, Unsteady, Viscous dissipation, Suction, Fourth-grade fluid

Abstract

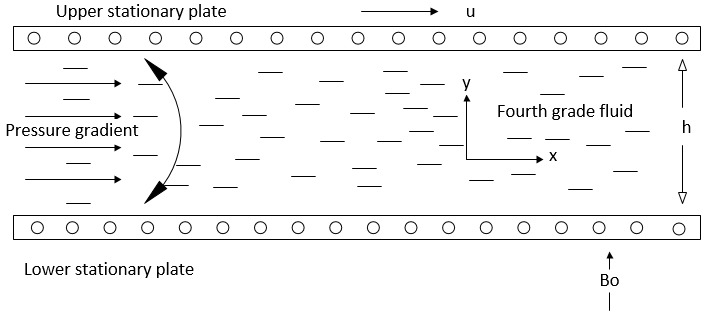
The unsteady magnetohydrodynamics (MHD) flow of fourth grade fluid between horizontal stationary plates with viscous dissipation and suction effects has been investigated. The fluid is subjected to a uniform transverse magnetic field. The upper and lower plates are stationary.   The partial differential equations that govern the flow are the momentum and energy equations. For the solution of the fluid flow model, the He- Laplace method was employed. The effect of various flow parameters on velocity and temperature profile were obtained. Investigated were the effects of suction parameter, third and fourth grade parameters and Hartman number on velocity profile. Graph were plotted for each case considered. Results of this research show that temperature field increases with increase in Eckert number and radiation parameter but decrease with increases in suction parameter and Prandtl number. While for velocity field, it is observed that it decreases with increase in suction parameter and Hartman number, but increases with increase in third and fourth grade parameters. The result of this research would be useful in Engineering fields such as Bioengineering enhance oil recovery and medical science of complex fluid in development of magnetic device for cell separation and targeted transport of drugs carriers, etc.

Dimensions

Arifuzzaman, S. M., Shakhaoth, K. Md., Al-Mamum, A., Reza- E-Rabbi, S. K., Biswas, P. and Karim, I. (2019). Hydrodynamic Stability and Heat and Mass Transfer Flow Analysis of MHD Radiative Fourth-Grade Fluid Through porous Plate with Chemical Reaction. Journal of King Saud University, 31(4), 1388 – 1398.

Aziz, T. & Mahomed, F. M. (2013). Reductions and Solutions for the Unsteady Flow of Fourth-Grade Fluid on a Porous Plate. Appli. Maths. Comput., 219, 9187 – 9195.

Bastian, E. R. (2017). Microfluidics: Modelling, Mechanics and Mathematics, Elsevier Imprint.

Bhatti, M. M. & Rashidi, M. M. (2016). Effects of Thermo-diffusion and Thermal Radiation on Williamson Nano Fluid over a Porous Shrinking/Stretching Sheet. J. Mol. Liq., 221, 567 – 573.

Cengel Y. A. (2003). Heat and mass transfer: a practical approach, 3rd edn. McGraw-Hill, Boston.

Chhabra, R. P. & Richard, S. F. (2008). Non – Newtonian Flow and Applied Rheology. 2ndedtion, Butterworth – Heinemann.

Cole, B.D. & Noll, W. (1960). An Approximation Theorem for Functionals with Applications in Continuum Mechanics. Arch. Ration. Mech. Anal., 6, 355 – 370.

Dunn, J. E. & Rajagopal, K. R. (1995) Fluids of Differential Type: Critical Review and Thermodynamic Analysis. International Journal of Engineering Science, 33(5), 689 – 729.

Ellahi, R., Zeeshan, A., Shehzad, N. & Alauri, S. Z. (2018). Structural Impact of Kerosene – Al2O3 Nano Liquid on MHD Poiseuille Flow with Variable Thermal Conductivity: Application of Cooling Process. J. Mol. Liq., 264, 607 – 615.

Frank, M. W. (1990). Fluid Mechanics, Fourth Edition McGraw HillFourier (1822). TheorieAnalytique de la Chaleurin

Ghorbani, A. (2009). Beyond Adomian Polynomials: He’s Polynomials. Chaos Solutions and Fractions, 39(3), 1486 – 1492.

Ghorbani, A. & Saberi-Nadjafi, J. (2007). He’s Homotopy Perturbation Method for Calculating Adomian Polynomials. International Journal of Nonlinear Science and Numerical Simulation, 8, 229 – 232.

Hayat, T., Wang, Y. & Hutter, K. (2002). Flow of a Fourth-Grade Fluid. Math.Models Methods Appl. Sci., 12, 797 – 811.

Hayat, T., Kara, A. H., & Momoniat, E. (2005). The Unsteady Flow of a Fourth-Grade Fluid Past a Porous Plate. Mathematical and Computer Modeling, 41, 1347 – 1353.

Hradesh, K. M. & Atulya, K. N. (2012). He-Laplace Method for Linear and Nonlinear Partial Differential Equations. Hindawi Publishing Corparation Journal of Applied Mathematics, 20, 1 – 16.

Huigol, R. (1975). Continuum Mechanics of Viscoelastic Liquid, Hindusthan.

Idowu, A.S & Sani, U. (2019). Thermal Radiation and Chemical Reaction Effects on Unsteady MagnetohydrodynamicThird Grade Fluid Flow Between Stationary and Oscillating Plates. International Journal of Applied Mechanics and Engineering, 24(2), 269 – 293.

Islam, S., Bano, Z., Siddique, I. & Siddiqui, A. M. (2011). The Optimal Solutions for the Flow of a Fourth-Grade Fluid with Partial Slip. Computer and Mathematics with Application, 6, 1507 – 1516.

Joseph, K. M., Ayankop, A. E. & Muhammed, S. U. (2021). Unsteady (MHD) Flow of Fourth Grade Fluid in a Horizontal Parallel Plates Channel with Suction Effect. International journal of applied mechanics and engineering, 26, 77 – 98.

Khan, Z., Khan, I., Ullah, M. & Tlili, I. (2018). Effect of Thermal Radiation and Chemical Reaction on non – Newtonian Fluid through a Vertically Stretching Porous Plate with Uniform Suction. Results in Physics, 9, 1086 – 1095.

Kodi, R., Vaddemani, R. R., Khan, M. I., Abdullaev, S. S., Habibullah, Boudjemline, A., Boujelbene, M., & Bouazzi, Y. (2023). Unsteady magneto-hydro-dynamics flow of Jeffrey fluid through porous media with thermal radiation, Hall current and Soret effects. Journal of Magnetism and Magnetic Materials, 582, 171033. https://doi.org/10.1016/j.jmmm.2023.171033

Mahabaleshwar, U. S., Maranna, T., Pérez, L. M., & Nayakar, S. N. R. (2023). An effect of Magnetohydrodynamic and Radiation on Axisymmetric Flow of non-Newtonian Fluid Past a Porous Shrinking/Stretching Surface. Journal of Magnetism and Magnetic Materials, 571, 170538. https://doi.org/10.1016/j.jmmm.2023.170538

Moakher, G. R., Abbasi, M. & Khaki, M. (2016). Fully Developed Flow of Fourth-Grade Fluid through a Channel with Slip Condition in the Presence of a Magnetic Field. Journal of Applied Fluid Mechanics, 9(5), 2239 – 2245.

René, M. & Sergei, M. S. (2007). Julius Hartmann and His Followers: A Review on the Properties of the Hartmann Layer. Magnetohydrodynamics: Historical Evolution and Trends. Fluid Mechanics and Its Application, 80, 155 – 156.

Rehan, A.S., Islam, S. & Siddiqui, A.M. (2010). Couette and Poiseuille Flows for Fourth-Grade Fluids using Optimal Homotopy Asymptotic Method. World Applied Science Journal, 9(1), 1228 – 1236.

Rivlin, R. & Ericksen J. L., (1995). Stress Deformation Relations for Isotropic Materials. Journal of Rational Mechanic, 4, 323 – 425.

Sander, C. J. & Holman, J. P. (1972). Franz Grashof and the Grashof Number. Int. J. Heat Mass Transfer, 15(2), 562 – 563.

Santhosha, B., Younus, S., Kamala, G. & Ramana, M. MV. (2017). Radiation and Chemical Reaction Effects on MHD Free Convective Heat and Mass Transfer Flow of a Viscoselastic Fluid Past a Porous Plate with Heat Generation/Absorption. International Journal of Chemical Sciences, 15(3), 1 – 16.

Satya, P. V., Venkateswarlu, B. & Devika, B. (2015). Chemical Reaction and Heat Source Effect on MHD Oscillatory Flow in an Irregular Channel. Ain Shams Engineering Journal, 1 – 10.

Shehzad, N., Zeeshan, A., & Ellahi, R. (2018). Electroosmotic Flow of MHD Power Law Al2O3-PVC Nano Fluid in a horizontal Channel: Couette – Poiseuille Flow Model .Commu. Theor. Phys., 65, 655 – 666.

Taha, A., Magan, A. B., & Mahomed, F. M. (2015). Invariant Solutions for the Unsteady Magnetohydrodynamics (MHD) Flow of a Fourth-Grade Fluid Induced due to the Impulsive Motion of a Flat Porous Plate. Brazil Journal of Physics, 45, 120 – 131.

Taza, G., Fazle, G., Islam, S., Shah, R. A., Khan, I., Nasir, S. & Sharidan (2016). Unsteady Thin Film Flow of a Fourth-Grade Fluid over a Vertical Moving and Oscillating Belt. Propulsion and Power Research, 5(3), 223 – 235.

Truesdell, C. & Noll, W. (1992). The Nonlinear Field Theories of Mechanics. Springer, 2.

Truesdell, C. & Noll, W. (2004). The Nonlinear Field Theories of Mechanics. 3rd edition, Springer, USA.

Umavathi, J. C., Liu, I. C. & Meera, S. (2010). Unsteady Flow and Heat Transfer of Porous Media Sandwiched between Viscous Fluids. Applied Mathematics and Mechanics, 31(12), 1497 – 1516.

Wang, Y. & Wu, W. (2007). Unsteady Flow of a Fourth-Grade Fluid due to an Oscillation Plate. Int. J. Nonlinear Mech., (42), 432 – 441.

Zaman, H., Shah, M. A. & Ibrahim, M. (2013). Unsteady Incompressible Couette Flow Problem for the Eyring – Powell Model with Porous Walls. American Journal of Computational Mathematics, 3, 313 – 325.

Zaman, H., Abbas, T., Sohail, A. & Ali, A. (2014). Couette Flow Problem for an Unsteady MHD Fourth-Grade Fluid with Hall Currents. Journal of Applied Mathematics and Physics, 2, 1 – 10.

Physical Configuration of the Plane Poiseuille Flow

Published

04-11-2025

How to Cite

T. Zakari, N., E. Andi, A., K. Moses, J., A.A, W., & B. Hassan, J. (2025). UNSTEADY MAGNETOHYDRODYNAMICS (MHD) FLOW OF FOURTH GRADE FLUID BETWEEN HORIZONTAL STATIONARY PLATES WITH VISCOUS DISSIPATION AND SUCTION EFFECTS. FUDMA JOURNAL OF SCIENCES, 9(11), 345 – 355. https://doi.org/10.33003/fjs-2025-0911-4189

Issue

Vol. 9 No. 11 (2025): FUDMA Journal of Sciences - Vol. 9 No. 11

Section

Review Articles
Copyright & Licensing

Copyright (c) 2025 Nasiru T. Zakari, Ayankop E. Andi, Joseph K. Moses, Wachin A.A, Joshua B. Hassan

Creative Commons License

This work is licensed under a Creative Commons Attribution 4.0 International License.

How to Cite

T. Zakari, N., E. Andi, A., K. Moses, J., A.A, W., & B. Hassan, J. (2025). UNSTEADY MAGNETOHYDRODYNAMICS (MHD) FLOW OF FOURTH GRADE FLUID BETWEEN HORIZONTAL STATIONARY PLATES WITH VISCOUS DISSIPATION AND SUCTION EFFECTS. FUDMA JOURNAL OF SCIENCES, 9(11), 345 – 355. https://doi.org/10.33003/fjs-2025-0911-4189