ACCURATE BLOCK HYBRID METHODS FOR LARGE SCALE CHEMICAL KINETICSSIMULATIONS OF THE HIGH IRRADIANCE (HIRES) PROBLEM
DOI:
https://doi.org/10.33003/fjs-2025-0911-4073Keywords:
Hires Problem, Block Hybrid, Absolute Stability, Interpolation, Collocation, Exact SolutionAbstract
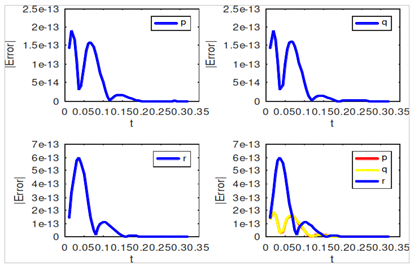
This article presents two A(a), zero–stable, consistent and convergent methods for the numerical approximation of the High Irraddiance problem. The first method is a first derivative method while the second method is a second derivative block hybrid method for the numerical solution of initial problems most especially the High Irraddiance (HIRES) problem with origins from chemical kinetics. The first method is of order five with a small region of absolute stability, while the new second derivative method is of order nine with a large region of absolute stability as well as smaller error constants. The methods stems from the interpolation and collocation approach with un-equidistant give points. Sequel to using the methods in solving the HIRES problem which has no exact solution, we compared the performance of our second method with a method in a recent literature and the method outperformed it. This gave us the motivation in using the method to solve the problem under consideration
References
Abdullahi H. (2018). Development of block unification hybrid linear multistep methods forfluid flow equations (Doctoral dissertation, Federal University of Technology, Minna).
Akinola R. O. and Akoh A. S. A Seventh–order computational algorithm for the solution of stiff systems of differential equations. Journal of the Nigerian Mathematical Society. Vol. 42, Issue 3, pp. 215 - 242, 2023.
Amat S, Maria Jose Legaz M. J. & Ruiz-Alvarez J(2019). On a Variational Method for Stiff Differential Equations Arising from Chemistry Kinetics. MDPI Mathematics, 7(5), 45– 49; https://doi.org/10.3390/math7050459
Bennett J. C., Krishnamoorthy V., Liu S., Grout R. W., Hawkes E. R., & Chen J. H. (2011). Feature-based statistical analysis of combustion simulation data. IEEE Transactions on Visualization and Computer Graphics, 17(12), 1822–1831.
Castro R., Bergonzi M., & Kofman E. (2024). Discrete-event simulation of continuous-time systems: Evolution and state of the art of quantized state system methods. Simulation, 100(6).
Hawagfeh N. S., & Kaya D. (2004). Comparing numerical methods for the solutions of systems of ordinary differential equations. Applied Mathematics Letters, 17(3), 323–328.
Henrici P., Discrete variable methods in ODE. New York, USA: John Wiley & Sons, 1962.
Jacobson, M. Z. (2005). Fundamentals of atmospheric modeling (2nd ed.). Cambridge University Press.
Kowalski K., Bair R., Bauman N. P., Boschen J. S., Bylaska E. J., Daily J., de JongW. A., Dunning Jr. T., Govind N., Harrison R. J., Keceli M., Keipert K., Krishnamoorthy S., Kumar S., Mutlu E., Palmer B., Panyala A., Peng B., Richard R. M., Straatsma T. P., Sushko P., Valeev E. F., Valiev M., van Dam H. J. J., Waldrop J. M., Williams-Young D. B., Yang C., Zalewski M., & Windus Lambert, J. D. Computational Methods in Ordinary Differential Equations; John Wiley: New York, NY, USA, 1973.
Lu T., & Law C. K. (2009). Toward accommodating realistic fuel chemistry in large-scale computations. Progress in Energy and Combustion Science, 35(2), 192–215.
Mashruk S., Shi H., Mazzotta L., Ustun C. E., Aravind B., Meloni R., Alnasif A., Boulet E., Jankowski R., Yu C., Alnajideen M., Paykani A., Maas U., Slefarski R., Borello D., & Valera- Medina A. (2024). Perspectives on NOx emissions and impacts from ammonia combustionprocesses. Energy & Fuels, 38(15), 19253–19292.
Okuonghae R. I. and Ikhile M. N. O., Continuous formulation of A(α)-Stable Second derivative linear multistep methods for Stiff initial value problems in ordinary differential equations.Journal of Algorithms and Computational Technology, 6, 175-–190.
Onumanyi, P., Awoyemi, D. O., Jator, S. N. and Sirisena, U. W. (1994) New Linear Multistep Methods with Continuous Coefficients for First Order Initial Value Problems. Journal of Nigeria Mathematics Society, 13, 37-51.
Rufai M. A. (2024). Numerical integration of third-order BVPs using a fourth-order hybrid block method. Journal of Computational Science, 81, 102338.
Simon H. D., Zacharia T. & Stevens R. L. (2007). Modeling and simulation at the exascale for energy and the environment. Lawrence Berkeley National Laboratory.
Singh G., Garg A., Singla R., & Kanwar V. (2021). A novel two-parameter class of optimize hybrid block methods for integrating differential systems numerically. Computational and Mathematical Methods, 3(6), e1214.
Smith, J., & Anderson, P. (2005). A First-Order Approach to High Irradiance Problems.” Journal of Photovoltaic Research, 12(3), 215–225.
Spiteri R. J. (1997). Solution methods for differential systems subject to algebraic inequality constraints (T). University of British Columbia. Retrieved from https://open.library.ubc.ca/collections/ubctheses/831/items/1.0080007
T. L. (2021). From NWChem to NWChemEx: Evolving with the computational chemistry landscape. Chemical Reviews, 121(10), 4962–4998.
Trieschmann J., Vialetto L., & Gergs T. (2023). Machine learning for advancing lowtemperature plasma modeling and simulation. Journal of Micro/Nanopatterning, Materials, and Metrology, 22(4), 041504.
Yakubu S. D. and Sibanda P. (2024) One–Step Family of Three Optimized Second–Derivative Hybrid Block Methods for Solving First–Order Stiff Problems. Hindawi Journal of Applied Mathematics Volume 2024, Article ID 5078943, https://doi.org/10.1155/2024/5078943
Zhang T., Yi Y., Xu Y., Chen Z. X., Zhang Y., & Xu, Z.-Q. J. (2022). A multi-scale sampling method for accurate and robust deep neural network to predict combustion chemical kinetics. Combustion and Flame 245 (2022) 112319.
Downloads
Published
Issue
Section
Categories
License
Copyright (c) 2025 Richard Olatokunbo Akinola, Shangkum Yildum Goji, Kyaharnan Victor Joshua, Amin Miracle Daze

This work is licensed under a Creative Commons Attribution 4.0 International License.




